之前小编为大家带来过我的世界标准化树场的速度计算这篇文章，不过之前的数据有些问题，所以特此为大家带来了一篇关于我的世界树场速度计算的修正版，希望大家能够喜欢哦！

　　作者：maple_in_thu

　　文件下载地址：

　　【修正说明】

　　由duoduo指出，在树场周期中，存在这样一个阶段，玩家可以放置树苗，骨粉也可以撒，但是上面伪递推还没完全收回，36号方块可以让玩家的右键穿过，但是会阻止树木生长。

　　因此在这个阶段中可以让树苗长到第一阶段（树苗长成树木经过2个生长阶段）

　　首先将树场设计参数化，将树场表述为3个参数。

　　1.从树场周期开始（树木长出的瞬间）到玩家可以右键放置树苗的时间 T1

　　2.从树场周期开始（树木长出的瞬间）到树木可以生成的时间T2（T2≥T1）

　　3.树场发射器数量N

　　其次树场的运行速度还有一个重要因素决定，即玩家放置树苗的时间。

　　根据源码中runTick函数，游戏的每个周期会先进行schedule时间的更新计算，其中包括了红石器件的延迟、活塞的运动归位等时间。接下来会处理玩家的鼠标键盘事件，而玩家的右键就是这个时候处理的。

　　因此每个gametick，36号方块变为真实方块、高频时钟运作驱动发射器发射长成树木等是在放置树苗之后执行的。

　　意味着玩家在T1时刻就可以放置树苗，但是在玩家放置树苗的同一个gt内发射器喷洒的骨粉不会作用到树苗上。而玩家在按住右键不放时，游戏会将右键输入频率设置为4 gt一次

　　所以再引入玩家对树场的一个参数：

　　从树场周期开始（树木长出的瞬间）到玩家放置树苗的时间Tp

　　显然Tp可以取4个值，T1、T1+1gt、T1+2gt、T1+3gt

　　以下讨论中，T1、T2、Tp均取gametick（0.05秒）为单位

　　现在速度就是由T1、T2、Tp决定的了

　　现在假设从Tp到T2之间有a次发射器发射（也就是有a个4的整数倍），当然如果T1≤Tp了，也就是放好树苗的时候已经进入了树木可以生成的阶段，a就是0

　　那么在a次发射中，树苗能长到第一阶段的概率p1=1-0.55^a

　　因此在T2之后，有p1的概率只要再长一个阶段，有1-p1的概率要长2个阶段

　　所以在T2之后要撒x次骨粉的概率可以写为这两部分的和，即

　　p2(x)=p1*(0.55^(x-1))*(0.45) + (1-p1)*(x-1)*(0.45^2)*(0.55^(x-2))

　　继续按照原贴的计算方式，计算T2之后发射器要喷洒y次的概率

　　py(y)=∑p2(N*y-i)，(i=0,1,2,...,N-1)

　　最后计算y的数学期望，也就是在T2之后平均要喷洒几次骨粉

　　ey=∑y*py(y)，(y=1,2,3,...,∞)

　　因此长成阶段，第一次撒骨粉的时刻Tb满足 Tb≥T2 同时因为撒骨粉必须在 Tb>Tp

　　Tb即满足上面两个条件的最小的4的整数倍。

　　Tb时刻撒完骨粉后，平均还需要ey-1次才能长成树木，每次撒骨粉的间隔为4，因此最终树场周期为Tb+4(ey-1)

　　这个计算过程略复杂，我写成了代码辅助计算，其中树场的参数有2个T1和T2，玩家的输入Tp有4个选项，会导致2种不同的结果，因此我们实际计算的时候以4中情况下速度的均值来计算。

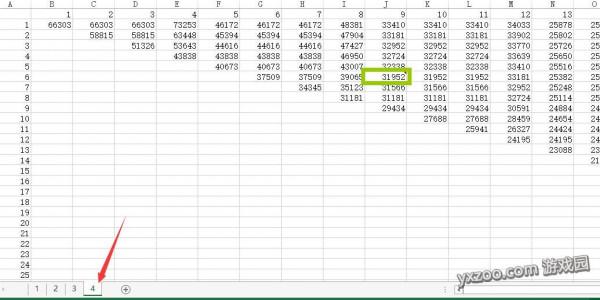
　　最终计算得到的结果由于数值太多，我做成了一个excel表格，大致如下

　　横坐标表示T2（从树木生成到下一个树木有足够空间可以生长的时间间隔）

　　纵坐标表示T1（从树木生成到下一个树苗可以被放置的时间间隔）

　　单位均为gametick，0.05秒

　　图中的数据值为考虑不同的Tb的均值，单位为wood/hour

　　文件共分成了4个sheet，表示发射器的数量。

　　之前小编为大家带来过我的世界标准化树场的速度计算这篇文章，不过之前的数据有些问题，所以特此为大家带来了一篇关于我的世界树场速度计算的修正版，希望大家能够喜欢哦！

　　作者：maple_in_thu

　　文件下载地址：

　　【修正说明】

　　由duoduo指出，在树场周期中，存在这样一个阶段，玩家可以放置树苗，骨粉也可以撒，但是上面伪递推还没完全收回，36号方块可以让玩家的右键穿过，但是会阻止树木生长。

　　因此在这个阶段中可以让树苗长到第一阶段（树苗长成树木经过2个生长阶段）

　　首先将树场设计参数化，将树场表述为3个参数。

　　1.从树场周期开始（树木长出的瞬间）到玩家可以右键放置树苗的时间 T1

　　2.从树场周期开始（树木长出的瞬间）到树木可以生成的时间T2（T2≥T1）

　　3.树场发射器数量N

　　其次树场的运行速度还有一个重要因素决定，即玩家放置树苗的时间。

　　根据源码中runTick函数，游戏的每个周期会先进行schedule时间的更新计算，其中包括了红石器件的延迟、活塞的运动归位等时间。接下来会处理玩家的鼠标键盘事件，而玩家的右键就是这个时候处理的。

　　因此每个gametick，36号方块变为真实方块、高频时钟运作驱动发射器发射长成树木等是在放置树苗之后执行的。

　　意味着玩家在T1时刻就可以放置树苗，但是在玩家放置树苗的同一个gt内发射器喷洒的骨粉不会作用到树苗上。而玩家在按住右键不放时，游戏会将右键输入频率设置为4 gt一次

　　所以再引入玩家对树场的一个参数：

　　从树场周期开始（树木长出的瞬间）到玩家放置树苗的时间Tp

　　显然Tp可以取4个值，T1、T1+1gt、T1+2gt、T1+3gt

　　以下讨论中，T1、T2、Tp均取gametick（0.05秒）为单位

　　现在速度就是由T1、T2、Tp决定的了

　　现在假设从Tp到T2之间有a次发射器发射（也就是有a个4的整数倍），当然如果T1≤Tp了，也就是放好树苗的时候已经进入了树木可以生成的阶段，a就是0

　　那么在a次发射中，树苗能长到第一阶段的概率p1=1-0.55^a

　　因此在T2之后，有p1的概率只要再长一个阶段，有1-p1的概率要长2个阶段

　　所以在T2之后要撒x次骨粉的概率可以写为这两部分的和，即

　　p2(x)=p1*(0.55^(x-1))*(0.45) + (1-p1)*(x-1)*(0.45^2)*(0.55^(x-2))

　　继续按照原贴的计算方式，计算T2之后发射器要喷洒y次的概率

　　py(y)=∑p2(N*y-i)，(i=0,1,2,...,N-1)

　　最后计算y的数学期望，也就是在T2之后平均要喷洒几次骨粉

　　ey=∑y*py(y)，(y=1,2,3,...,∞)

　　因此长成阶段，第一次撒骨粉的时刻Tb满足 Tb≥T2 同时因为撒骨粉必须在 Tb>Tp

　　Tb即满足上面两个条件的最小的4的整数倍。

　　Tb时刻撒完骨粉后，平均还需要ey-1次才能长成树木，每次撒骨粉的间隔为4，因此最终树场周期为Tb+4(ey-1)

　　这个计算过程略复杂，我写成了代码辅助计算，其中树场的参数有2个T1和T2，玩家的输入Tp有4个选项，会导致2种不同的结果，因此我们实际计算的时候以4中情况下速度的均值来计算。

　　最终计算得到的结果由于数值太多，我做成了一个excel表格，大致如下

　　横坐标表示T2（从树木生成到下一个树木有足够空间可以生长的时间间隔）

　　纵坐标表示T1（从树木生成到下一个树苗可以被放置的时间间隔）

　　单位均为gametick，0.05秒

　　图中的数据值为考虑不同的Tb的均值，单位为wood/hour

　　文件共分成了4个sheet，表示发射器的数量。